2.4 Adjacency matrix

The adjacency matrix of a network that has $N$ nodes has $N$ rows and $N$ columns. If there is a link from node $i$ to node $j$, then $A_{i}j=1$. If node $i$ and node $j$ are not connected, then $A_{i}j=0$.

For an undirected network, the link $(i,j)$ has two representations: $A_{i}j$ = $A_{j}i$. That’s why the adjacency matrix of an undirected network is always symmetric.

Lets have a look at the adjacency matrix of g1 and g2.

For g1:

par(mar = c(1, 1, 1, 1))
plot(g1)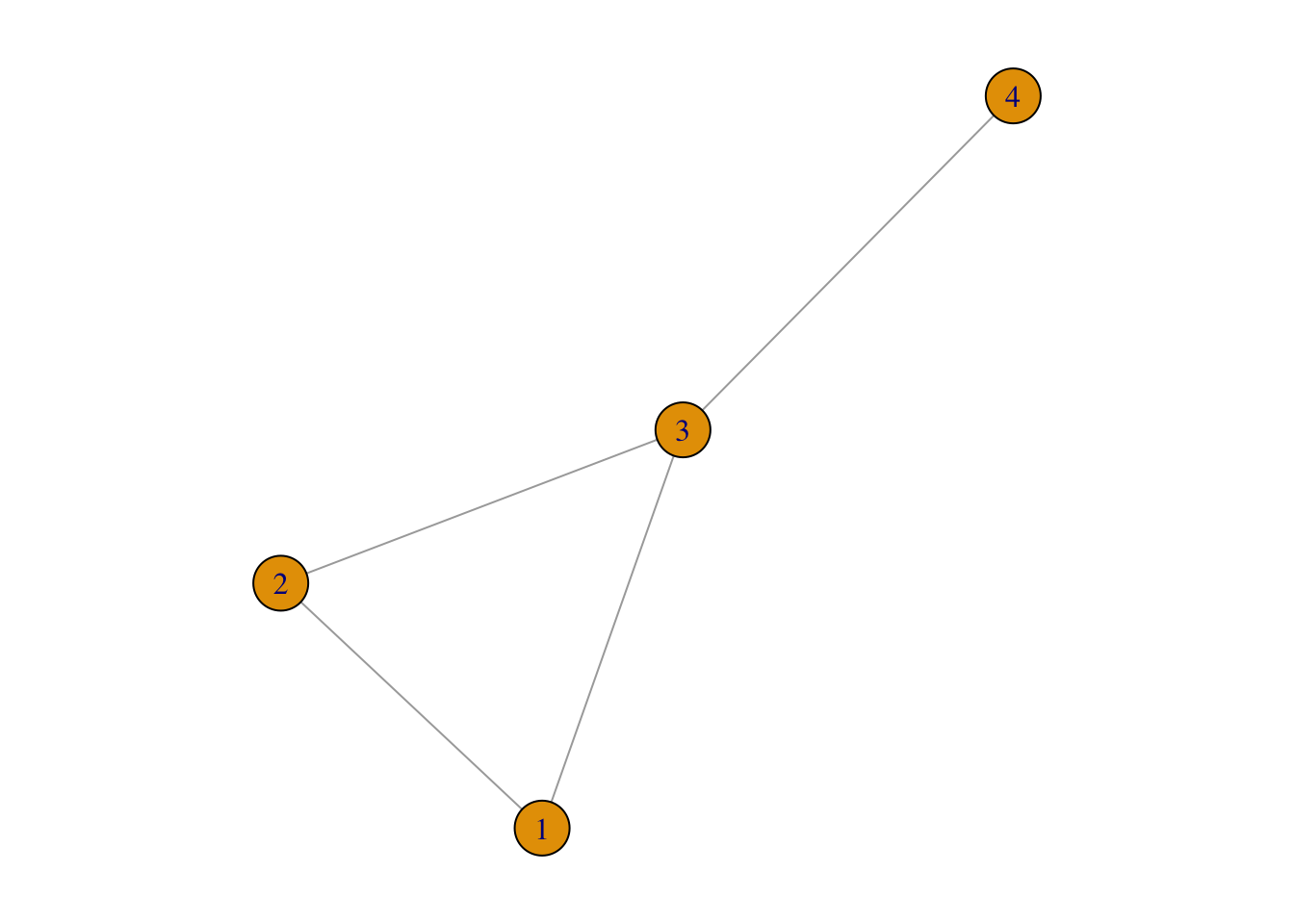

as_adjacency_matrix(g1)

## 4 x 4 sparse Matrix of class "dgCMatrix"
##             
## [1,] . 1 1 .
## [2,] 1 . 1 .
## [3,] 1 1 . 1
## [4,] . . 1 .

For g2:

par(mar = c(1, 1, 1, 1))
plot(g2)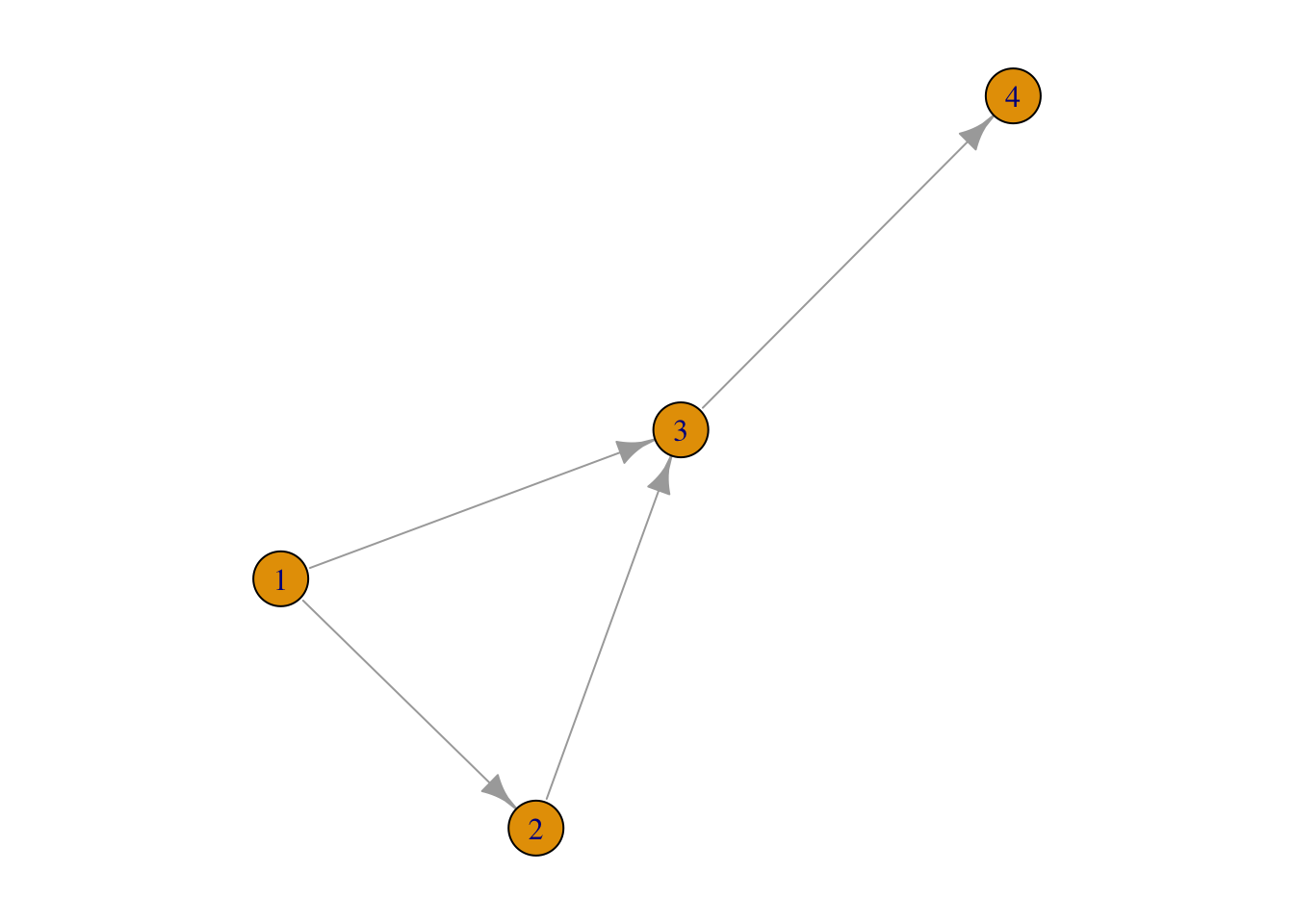

as_adjacency_matrix(g2)

## 4 x 4 sparse Matrix of class "dgCMatrix"
##             
## [1,] . 1 1 .
## [2,] . . 1 .
## [3,] . . . 1
## [4,] . . . .

Each dot in the matrix means $0$. The adjacency matrices here did not label the column name. To better understand it, you can imagine that the columns are also labeled as [1, ], [2, ], [3, ] and [4, ] as the rows are.